Shell Sort (셸 정렬)
- 주어진 간격(일반적으로 k)만큼 떨어진 서브배열을 만들어 삽입정렬을 수행한다.
- 시간복잡도는 평균적으로 O(n log n), 최고 O(n), 최악의 경우 O(n^2)의 시간복잡도를 가지고 있다. 간격에 따른 성능이 제각각이라 시간복잡도 분석이 쉽지 않다.
- 간격은 홀수로 지정하여, 간격이 절반으로 줄어들 때 짝수가 나오면 +1을 하여 홀수로 만든다.

def gapInsertionSort(x, start, gap):
for target in range(start+gap, len(x), gap):
val = x[target]
i = target
while i > start:
if x[i-gap] > val:
x[i] = x[i-gap]
else:
break
i -= gap
x[i] = val
return x
def shellSort(x):
gap = len(x)//2
print(gap)
while gap > 0:
for start in range(gap):
gapInsertionSort(x, start, gap)
gap = gap//2
return x
if __name__ == '__main__':
x = [4,5,2,1,8,3,6,9,7]
print(shellSort(x))Merge Sort (병합 정렬)
- 두개의 배열로 쪼개는 작업을 반복한 뒤, 쪼갠 순서의 반대로 작은 값부터 병합해 나가는 분할 정복 알고리즘이다.
- 시간복잡도는 두개의 배열로 쪼개는 데 O(log n) (이진탐색) 이고, 데이터 병합이 O(n)이므로, 정렬 상태와 무관하게 언제나 O(n log n)이다. 데이터 크기만한 메모리가 더 필요한 것이 단점이다.
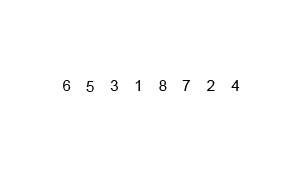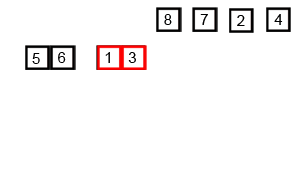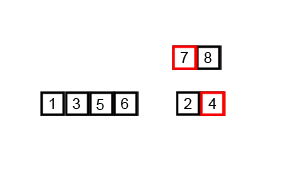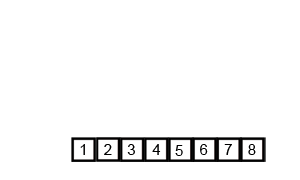
def mergeSort(x):
if len(x) > 1:
mid = len(x)//2
lx, rx = x[:mid], x[mid:]
mergeSort(lx)
mergeSort(rx)
li, ri, i = 0, 0, 0
while li < len(lx) and ri < len (rx):
if lx[li] < rx[ri]:
x[i] = lx[li]
li += 1
else:
x[i] = rx[ri]
ri += 1
i += 1
x[i:] = lx[li:] if li != len(lx) else rx[ri:]
return x
if __name__ == '__main__':
x = [4,2,5,1,3,6]
print(mergeSort(x))Quick Sort (퀵 정렬)
- 피벗(pivot, 기준값)을 정하여 피벗보다 작은 값은 피벗 앞쪽에, 피벗보다 큰 값은 피벗 뒤쪽에 오도록 한다. 피벗 양 쪽 배열에 대해 같은 작업을 반복한다. 분할 정복 방법의 일종이며 재귀 호출이 진행될 때마다 최소한 하나의 피벗은 최종적으로 위치가 정해진다.
- 시간복잡도는 데이터를 절반씩 쪼갠다면 O(log n)이고, n개의 값을 피봇과 비교하므로 O(n log n)이다. 피봇 선정 기준에 따라 쪼개는 위치가 한 쪽에 치우쳐 있을 수도 있다. (데이터가 이미 정렬되어 있고, 맨 끝 원소를 피봇으로 선정하는 경우) 이 때는 쪼개는 비용이 O(n)이므로 퀵 정렬의 시간복잡도가 O(n^2)까지 등가한다. 재귀 호출을 위한 스택을 사용하므로 추가 메모리가 필요하다.
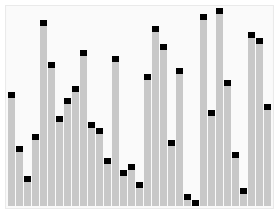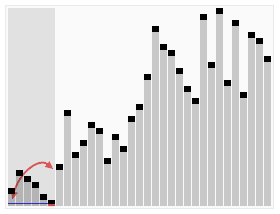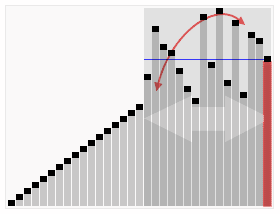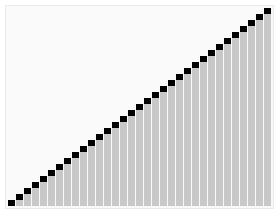
def swap(x, i, j):
x[i], x[j] = x[j], x[i]
def pivotFirst(x, lmark, rmark):
pivot_val = x[lmark]
pivot_idx = lmark
while lmark <= rmark:
while lmark <= rmark and x[lmark] <= pivot_val:
lmark += 1
while lmark <= rmark and x[rmark] >= pivot_val:
rmark -= 1
if lmark <= rmark:
swap(x, lmark, rmark)
lmark += 1
rmark -= 1
swap(x, pivot_idx, rmark)
return rmark
def quickSort(x, pivotMethod=pivotFirst):
def _qsort(x, first, last):
if first < last:
splitpoint = pivotMethod(x, first, last)
_qsort(x, first, splitpoint-1)
_qsort(x, splitpoint+1, last)
_qsort(x, 0, len(x)-1)
return x
if __name__ == '__main__':
x = [4,2,5,1,3,6]
print(quickSort(x))참조
- https://namu.wiki/w/정렬%20알고리즘
- https://en.wikipedia.org/wiki/Sorting_algorithm
- http://www.b3ta.com/board/10454738
- https://interactivepython.org/runestone/static/pythonds/index.html#
- http://ejklike.github.io/2017/03/04/sorting-algorithms-with-python.html
- https://gmlwjd9405.github.io/2018/05/08/algorithm-shell-sort.html
'Programming > Algorithm' 카테고리의 다른 글
| [프로그래머스] 스택/큐 주식가격 (with.python) (0) | 2021.09.08 |
|---|---|
| [프로그래머스] 스택/큐 프린터 (with.python) (1) | 2021.09.07 |
| [프로그래머스] 스택/큐 기능개발 (with.python) (0) | 2021.09.06 |
| Sorting (1) - 정렬 알고리즘 구현하기 (Bubble, Selection, Insertion) (with.Python) (0) | 2021.06.28 |

댓글